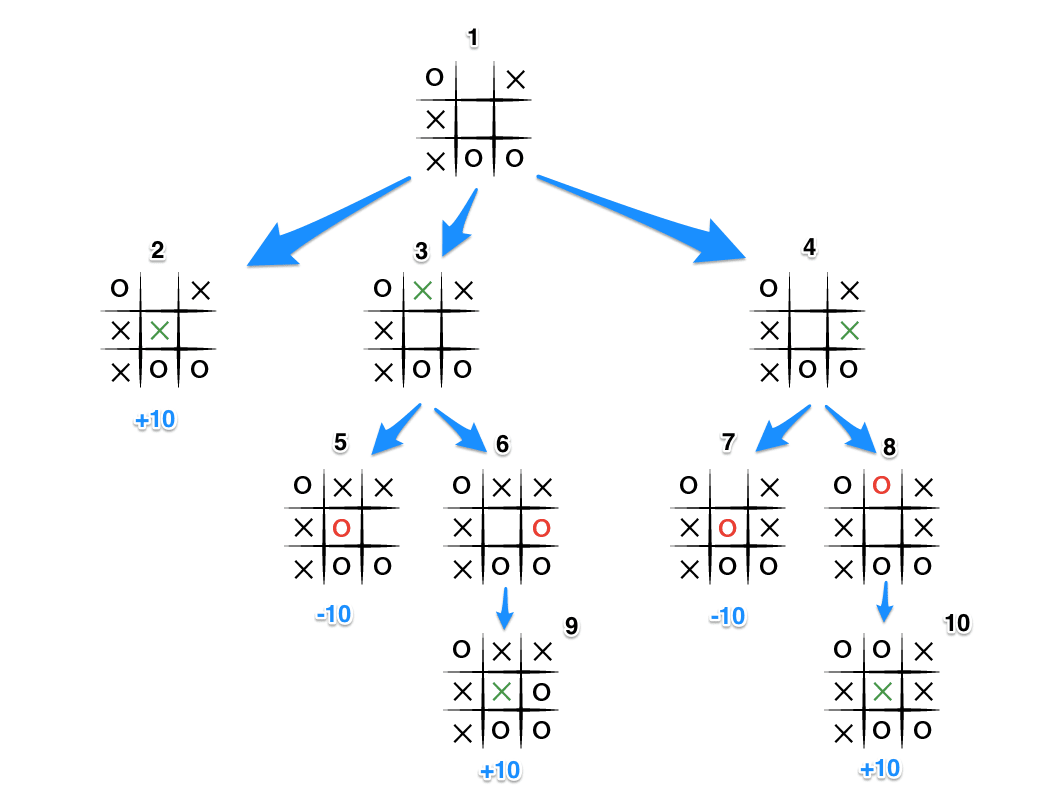
Tic-Tac-Toe was my first hands-on project in adversarial AI. On the surface, it looks almost too trivial to be interesting. Yet, precisely because it is so simple, it became the perfect entry point into the world of decision-making algorithms. This project was my first encounter with the Minimax algorithm, and it taught me how recursive search can mimic intelligent behaviour in ways that appear surprisingly lifelike. Although the game itself is “solved” and every outcome can be predicted, working through the mechanics gave me a framework for thinking about games, strategies, and how agents anticipate each other’s actions.
Problem Statement / Motivation
I was introduced to AI concepts through Robert Miles’ discussions of AI safety, where examples like Tic-Tac-Toe are used to show how systems can be both simple and profound. I wanted to explore this duality: how a child’s game could illustrate such deep computational principles. My motivation was not to make the strongest Tic-Tac-Toe agent possible, but rather to understand why optimal play is guaranteed, how algorithms discover it, and what this says about adversarial reasoning more generally. Building this project gave me a tangible sense of how deterministic systems can create the illusion of adaptive, almost human-like decisions.
Features & Technical Details
- Minimax Algorithm in Depth: The Minimax algorithm is built on the idea of anticipation. In a two-player, zero-sum environment, every move I make is assumed to be countered by the opponent’s best possible move. This forces the agent to simulate not only its own decisions but also the opponent’s responses. The recursive logic flows downward through the game tree, exploring all possible continuations, then flows upward as the algorithm assigns scores to each move based on the eventual outcomes.
Where is the new state reached by applying action in state .
In practical terms, the program generates the full game tree of Tic-Tac-Toe, evaluates terminal states (wins, losses, draws), and propagates those results upward to inform earlier moves. Because the state space is so small, the algorithm can search exhaustively with ease.
* If it’s my turn, the algorithm maximizes the score: it selects the action that yields the highest value in the long run. * If it’s the opponent’s turn, the algorithm minimizes the score: it assumes the opponent will always try to reduce my advantage. Mathematically, we can write the recursive definition as: * **Game Mechanics:** * Tic-Tac-Toe is a perfect-information, zero-sum game. Both players see the entire board, and no randomness is involved. * The limited size of the game tree ensures exhaustive search is feasible without optimization. * **Interface:** * I implemented the game as a simple Java command-line interface. While minimal, it was enough to allow quick iteration, human-vs-AI play, and testing of the algorithm’s logic. ### Results / Observations The AI played optimally every time. Against it, human players could never win; the best they could do was draw. While this was expected—Tic-Tac-Toe is solved—the fascination came from observing how the algorithm mirrored “strategic thought.” The recursive process gave the impression that the AI was deliberately setting traps or defending against threats, when in reality it was simply evaluating all outcomes. This was my first encounter with the idea that *intelligence can emerge from brute-force systematicity*. ### Potential Future Work While the classic 3x3 Tic-Tac-Toe board is fully solved, the project opens up many avenues for extensions: * **Larger Boards:** Exploring 4x4 or 5x5 variants would quickly expand the search tree and make heuristics or pruning necessary. * **Imperfect Information:** Adding twists such as hidden moves or randomized openings could transform the game into an environment where uncertainty plays a role. * **Graphical Interface:** A simple GUI would make the experience more engaging and demonstrate the AI’s play visually. ### Other Curiosities This project provided the intellectual scaffolding for everything that followed. Minimax here was straightforward; in Connect Four, the state space exploded and forced me to learn about pruning and heuristics. In Gomoku, the problem escalated again, requiring adaptive structures like a MemoryMap to bias exploration. By the time I reached BitSnake, I was thinking not only about turn-based adversaries but also about simultaneous, multi-agent decision-making. Tic-Tac-Toe was the seed from which all of this grew. It taught me that even a “solved” game could be an invaluable teacher when viewed through the lens of computational strategy.